Définition
Les fonctions trigonométriques ne sont pas subjectives sur \(\Bbb R\)
\(\longrightarrow\) pour définir l'inverse de ces fonctions, il faut une restriction : $$\cos:[0;\pi]\to[-1;1]$$
Maintenant nous avons une bijection. On peut ainsi construire la fonction réciproque de \(\cos\)
La réciproque de la fonction \(\cos\) est la fonction $${{\arccos}}:{{[-1;1]}}\to{{[0,\pi]}}$$
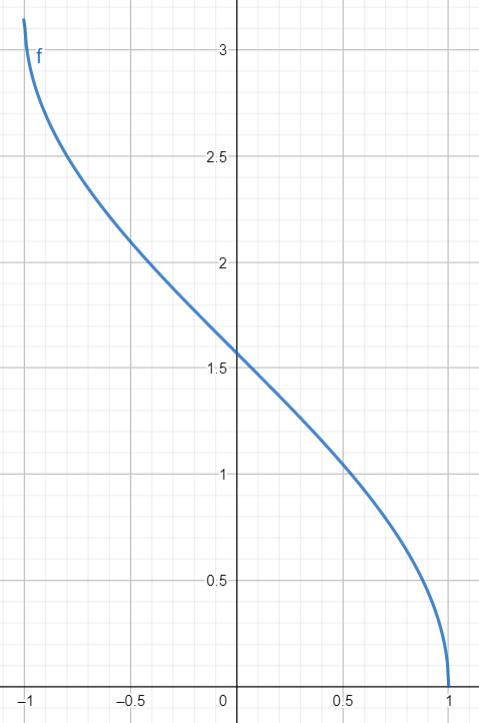
(
Bijection,
Fonction réciproque)
Formules utiles
Dérivée
$$({{\arccos x}})'={{\frac{-1}{\sqrt{1-x^2} } }}$$
Valeurs particulières
$$\arccos\left({{1}}\right)={{0}}$$
$$\arccos\left({{\frac{\sqrt3}2}}\right)={{\frac\pi6}}$$
$$\arccos\left({{\frac1{\sqrt2} }}\right)={{\frac\pi4}}$$
$$\arccos\left({{\frac12}}\right)={{\frac\pi3}}$$
$$\arccos\left({{0}}\right)={{1}}$$
